Recursion#
Recursion is a method of solving problems that involves breaking a problem down into smaller and smaller subproblems until you get to a small enough problem that it can be solved trivially.
Usually recursion involves a function calling itself, recursion allows us to write elegant solutions to problems that may otherwise be very difficult to program.
Three Laws of Recursion#
All recursive algorithms must obey three important laws:
A recursive algorithm must have a base case.
A recursive algorithm must change its state and move toward the base case.
A recursive algorithm must call itself, recursively.
A base case is typically a problem that is small enough to solve directly.
To obey the second law, we must arrange for a change of state that moves the algorithm toward the base case. A change of state means that some data that the algorithm is using is modified. Usually the data that represents our problem gets smaller in some way.
The final law is that the algorithm must call itself. This is the very definition of recursion, functions are good because you can take a large problem and break it up into smaller problems. The logic of recursion is an elegant expression of solving a problem by breaking it down into a smaller and easier problems.
def convert_to_base(n, base):
base_digits = "0123456789ABCDEF"
if n < base:
return base_digits[n]
else:
return convert_to_base(n//base,base) + base_digits[n%base]
print(convert_to_base(10, 2))
print(convert_to_base(1453, 16))
1010
5AD
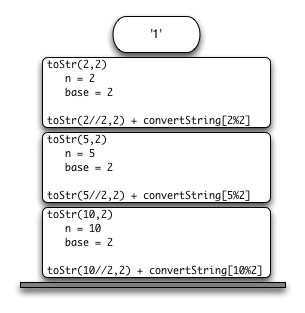
Stack Frames: Implementing Recursion#
When a function is called in Python, a stack frame is allocated to handle the local variables of the function. When the function returns, the return value is left on top of the stack for the calling function to access.
def toStr(n,base):
convertString = "0123456789ABCDEF"
if n < base:
return convertString[n]
else:
return toStr(n//base,base) + convertString[n%base]
print(toStr(10, 2))
Visualizing Recursion#
Fractals come from a branch of mathematics, and have much in common with recursion. The definition of a fractal is that when you look at it the fractal has the same basic shape no matter how much you magnify it. Some examples from nature are the coastlines of continents, snowflakes, mountains, and even trees or shrubs.
Sierpinski Triangle#
Sierpinski triangle illustrates a three-way recursive algorithm. The procedure for drawing a Sierpinski triangle by hand is simple. Start with a single large triangle. Divide this large triangle into four new triangles by connecting the midpoint of each side. Ignoring the middle triangle that you just created, apply the same procedure to each of the three corner triangles. Each time you create a new set of triangles, you recursively apply this procedure to the three smaller corner triangles. You can continue to apply this procedure indefinitely if you have a sharp enough pencil.
Complex Recursive Problems#
Tower of Hanoi#
The Tower of Hanoi puzzle was invented by the French mathematician Edouard Lucas in 1883. He was inspired by a legend that tells of a Hindu temple where the puzzle was presented to young priests. At the beginning of time, the priests were given three poles and a stack of 64 gold disks, each disk a little smaller than the one beneath it. Their assignment was to transfer all 64 disks from one of the three poles to another, with two important constraints. They could only move one disk at a time, and they could never place a larger disk on top of a smaller one. The priests worked very efficiently, day and night, moving one disk every second. When they finished their work, the legend said, the temple would crumble into dust and the world would vanish.
def tower_of_hanoi(num_discs, source, destination, auxiliary):
if num_discs >=1:
tower_of_hanoi(num_discs - 1, source, auxiliary, destination)
print(f"Move disc from {source} to {destination}")
tower_of_hanoi(num_discs - 1, auxiliary, destination, source)
tower_of_hanoi(3, "A", "B", "C")
Move disc from A to B
Move disc from A to C
Move disc from B to C
Move disc from A to B
Move disc from C to A
Move disc from C to B
Move disc from A to B


